Calcul de l'aire d'une pyramide

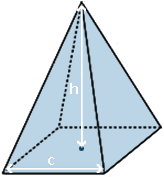
Formule de l'aire d'une pyramide à base carrée

Une pyramide à base carrée est un solide géométrique formé en reliant les sommets d’une base carrée à un point appelé apex. Elle fait partie de la famille des polyèdres et possède 5 faces : 1 base carrée et 4 faces triangulaires.

Pour calculer l’aire de la surface totale d’une pyramide à base carrée, la formule est la suivante :

A = (Côté × 4) × v(Hauteur² + (Côté/2)²) / 2

Où :
Côté = longueur d’un côté de la base carrée
Hauteur = distance verticale entre la base et l’apex

Comment fonctionne la formule

La formule calcule l’aire totale en additionnant l’aire de la base carrée et l’aire des 4 faces triangulaires. La racine carrée permet de déterminer la hauteur inclinée de chaque face triangulaire.

Exemple de calcul

Pour une pyramide avec un côté de 5 cm et une hauteur de 10 cm :
A = (5 × 4) × v(10² + (5/2)²) / 2
A = 20 × v(100 + 6,25) / 2
A = 20 × 10,31 / 2
A ˜ 103,1 cm²

Applications et usages pratiques

Les pyramides à base carrée sont utilisées dans plusieurs domaines, tant scientifiques que pratiques :

• Architecture et construction : modélisation de toits, monuments et pyramides classiques.
• Mathématiques et enseignement : étude des solides réguliers, calculs d’aires et volumes.
• Design et artisanat : modèles décoratifs, boîtes pyramidales, sculptures et maquettes.

Astuce de calcul rapide dans Excel ou Google Sheets

Pour calculer l’aire d’une pyramide rapidement dans un tableur :

1. Dans une cellule, entrez la valeur du côté de la base (ex. A1 : 5).
2. Dans une autre cellule, entrez la hauteur verticale (ex. B1 : 10).
3. Dans une troisième cellule, saisissez la formule :
   =(A1*4)*SQRT(B1^2+(A1/2)^2)/2
4. Appuyez sur Entrée : la cellule affichera directement l’aire totale de la pyramide en unités carrées.

Vous pouvez modifier les valeurs dans A1 et B1 pour recalculer rapidement l’aire de différentes pyramides.

Questions fréquentes

1. Quelle est la différence entre une pyramide à base carrée et une pyramide à base triangulaire ?
   La base carrée possède 4 côtés et 4 faces triangulaires, tandis que la base triangulaire possède 3 côtés et 3 faces triangulaires.
2. Comment calculer l’aire si on ne connaît que la hauteur inclinée des faces ?
   Vous pouvez mesurer la hauteur inclinée (apothème) et utiliser l’aire des triangles directement : A_face = (Côté × Apothème) / 2.
3. Peut-on appliquer cette formule à une pyramide de plus grande base ?
   Oui, la formule fonctionne pour toute pyramide à base carrée, quelle que soit la taille du côté et de la hauteur.